다익스트라(Dijkstra) 알고리즘 이론과 파이썬 구현
다익스트라(Dijkstra) 알고리즘
다익스트라(Dijkstra) 알고리즘은 특정한 하나의 시작 정점에서 모든 다른 정점까지의 최단 경로를 찾는 탐색 알고리즘입니다.
최단 경로는 경로의 길이순으로 구해집니다.
경로는 간선으로 주어지는데 이때 간선의 가중치는 문제에서 비용, 거리, 시간 등으로 나타납니다.
다익스트라(Dijkstra) 알고리즘의 과정입니다.
1. 하나의 시작 정점을 설정하고 이를 기준으로 각 최소 비용을 배열에 저장합니다.
바로 갈 수 없는 곳의 값은 INF로 합니다.
2. 방문하지 않은 점 중 가장 비용이 적은 정점을 선택합니다.
3. 해당 정점를 거쳐 특정한 정점으로 가는 경우를 고려하여 최소비용을 변경합니다.
4. 위의 과정을 반복해 최단 경로를 탐색합니다.

다음과 같은 단방향 그래프가 있으면 정점은 1, 2, 3, 4, 5, 6으로 6개입니다.
간선은 1 → 2, 1 → 3, 1 → 4, 2 → 6, 3 → 4로 5개입니다.
다익스트라 알고리즘은 시작점이 있어야 합니다. 1부터 모든 정점까지의 최단 경로를 탐색하겠습니다.
Dist는 1부터 각 정점까지의 최단 경로를 담는 배열입니다.
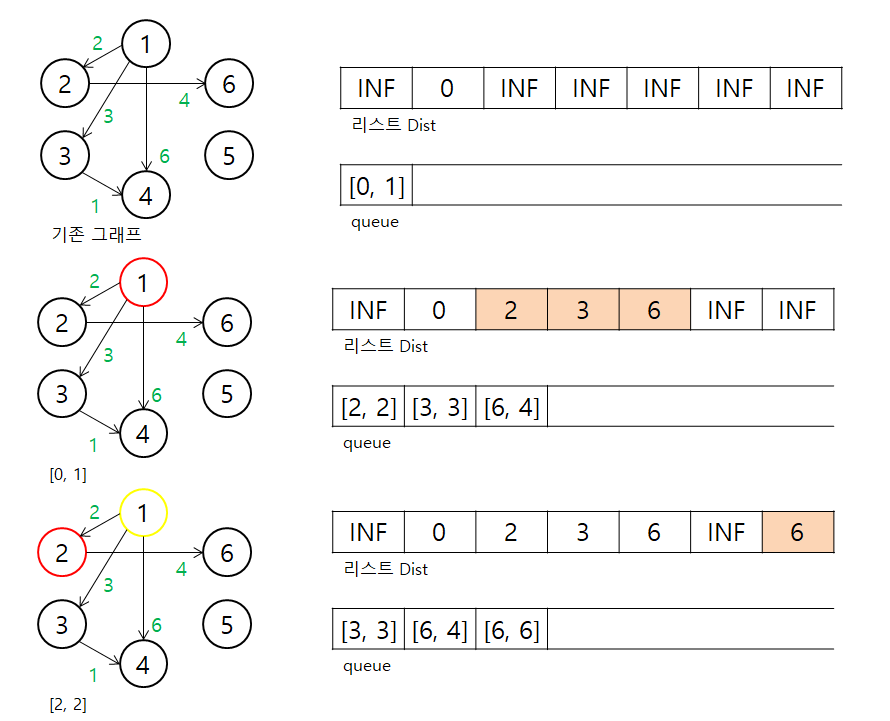
Dist에 1에서 1을 가는 경로는 0이기 때문에 Dist[1]은 0으로 설정해줍니다.
이 외의 값들은 아직 모르기 때문에 최대값을 넣습니다.
1에서 각 정점들의 최단 경로를 탐색에 Dist에 있는 값보다 작은 경우 최단 경로를 Dist에 넣습니다.
1에서 2로 가는 경로는 길이가 2이기 때문에 INF보다 적으니 Dist[2]는 2로 바꿔줍니다.
1에서 3로 가는 경로는 길이가 3이기 때문에 INF보다 적으니 Dist[3]는 3로 바꿔줍니다.
1에서 4로 가는 경로는 길이가 6이기 때문에 INF보다 적으니 Dist[4]는 6로 바꿔줍니다.
2에서는 1에서 2를 거쳐 6으로 가는 경로의 길이가 6이기 때문에 INF보다 적으니 Dist[6]는 6로 바꿔줍니다.
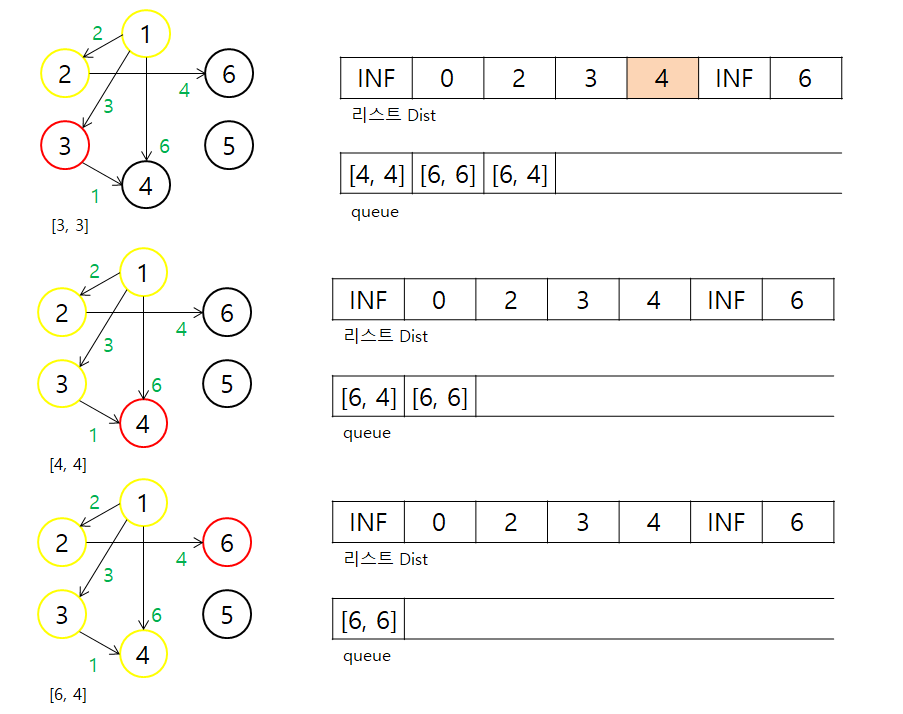
3에서는 1에서 3를 거쳐 4으로 가는 경로의 길이가 4인데 기존에 있던 6(1에서 4로 가는 경로) 보다 적으니 Dist[4]는 4로 바꿔줍니다.
4에서는 변경이 없습니다.
6에서는 변경이 없습니다.

다익스트라 알고리즘이 끝나면 정점 1, 2, 3, 4, 6을 거친 것을 알 수 있습니다.
정점 5를 연결해주는 간선은 없기 때문에 정점 5는 거치지 않았습니다.
최종적인 Dist가 1에서 각 정점까지의 최단 경로입니다.
Dist[0] 코드의 편리를 위해 만들었고 실제로는 정점도 없고 거치지 않았기 때문에 제외해야 합니다.
위의 예시를 이용한 다익스트라 알고리즘 파이썬 코드입니다.
import heapq
import sys
INF = sys.maxsize
def Dijkstra(adjacent, K):
dist = [INF] * len(adjacent) # source로부터의 최소 거리 배열, 무한대로 초기
dist[K] = 0 #시작점에서 시작점으로의 거리는 0으로 설정
queue = []
heapq.heappush(queue, [0, K]) #시작점 넣기
while queue:
# 거리가 제일 작은 노드 선택
current_dist, here = heapq.heappop(queue)
# 인접 노드 iteration
for there, length in adjacent[here].items():
next_dist = dist[here] + length
if next_dist < dist[there]:
dist[there] = next_dist
heapq.heappush(queue, [next_dist, there])
return dist
# v는 정점, e는 간선, k는 시작점
V=6
E=5
adjacent=[{}, {2: 2, 3: 3, 4: 6}, {6: 4}, {4: 1}, {}, {}, {}]
dist = Dijkstra(adjacent, 1)
for d in dist[1:]:
print(d if d != INF else "INF")
힙(heap) 큐 알고리즘을 이용한 기본 다익스트라 알고리즘 파이썬 코드입니다.
import heapq
import sys
INF = sys.maxsize
def Dijkstra(adjacent, K):
prev = [-1] * len(adjacent) # 이전에 거친 것 구하는 배열
dist = [INF] * len(adjacent) # K로부터의 최소 거리 배열, INF로 초기화
dist[K] = 0 #시작점에서 시작점으로의 거리는 0으로 설정
queue = []
heapq.heappush(queue, [0, K]) #시작점 넣기
while queue:
# 거리가 제일 작은 노드 선택
# current_dist: 현재까지의 거리, here : 지금 위치한 곳의 정점
current_dist, here = heapq.heappop(queue)
for there, length in adjacent[here].items():
next_dist = dist[here] + length
if next_dist < dist[there]:
dist[there] = next_dist
prev[there] = here
heapq.heappush(queue, [next_dist, there])
return dist, prev
# V는 정점 수, E는 간선 수, K는 시작점
V, E = map(int, input().split())
K = int(input())
adjacent = [{} for _ in range(V + 1)]
for i in range(E):
u, v, w = map(int, input().split())
#같은 경로의 간선이 주어질 경우 적은 비용의 간선 선택
if v in adjacent[u]:
adjacent[u][v] = min(adjacent[u][v], w)
else:
adjacent[u][v] = w
dist, prev = Dijkstra(adjacent, 1)
for d in dist[1:]:
print(d if d != INF else "INF")